数值分析重要插值公式
数值分析重要公式
插值
拉格朗日插值
拉格朗日插值多项式
n次插值基函数:(2.7)
$$
l_j(x_k)=
\begin{cases}
1,\space k=j,\
0,\space k≠j,
\end{cases}
\quad j,k=0,1,…,n
$$
这n+1个n次多项式$l_0(x),l_1(x),…,l_n(x)为节点x_0,x_1,…,x_n上的$n次插值基函数
具体表达式:(2.8)
$$
l_k(x)=\frac{(x-x_0)…(x-x_{k-1})(x-x_{k+1})…(x-x_n)}{(x_k-x_0)…(x_k-x_{k-1})(x_k-x_{k+1})…(x_k-x_n)},\quad k=0,1,…,n
$$
拉格朗日插值多项式:(2.9)
$$
L_n(x)=\sum^{n}_{k=0} y_k l_k(x)
$$
$l_k(x)为点x_k的插值基函数,y_k为点x_k对应的函数值,易得L_n(x_j)=y_j,j=0,1,…,n$
引入记号:(2.10)
$$
ω_{n+1}(x)=(x-x_0)(x-x_1)…(x-x_n)
\ ω^{‘}{n+1}(x_k)=(x_k-x_0)…(x_k-x{k-1})(x_k-x_{k+1})…(x_k-x_n)
$$
插值余项估计定理:(2.12)

牛顿插值
均差(差商)
1阶均差:
$$
f[x_0,x_k]=\frac{f(x_k)-f(x_0)}{x_k-x_0}
$$
2阶均差:
$$
f[x_0,x_1,x_k]=\frac{f[x_0,x_k]-f[x_0,x_1]}{x_k-x_1}
$$
k阶均差:(3.3)
$$
f[x_0,x_1,…,x_k]=\frac{f[x_0,…,x_{k-2},x_k]-f[x_0,x_1,…,x_{k-1}]}{x_k-x_{k-1}}
$$
均差的对称性:
$$
f[x_0,x_1,…,x_k]=f[x_1,x_0,x_2,…,x_k]=…=f[x_1,…,x_k,x_0]
$$
k阶均差另一表达(由对称性):(3.3)‘
$$
f[x_0,x_1,…,x_k]=\frac{f[x_1,x_2,…,x_k]-f[x_0,x_1,…,x_{k-1}]}{x_k-x_0}
$$
n阶均差与(n阶)导数的关系:(3.5)
$$
f[x_0,x_1,…,x_n]=\frac{f^{(n)}(ξ)}{n!},ξ∈[a,b].
$$
均差表:

牛顿插值多项式
牛顿均差插值多项式:(3.6)
$$
P_n(x)=f(x_0)+fx_0,x_1+fx_0,x_1,x_2(x-x_1)\+…+fx_0,x_1,…,x_n(x-x_1)…(x-x_{n-1})
$$
插值余项:(3.7)
$$
R_n(x)=f(x)-P_n(x)=f[x,x_0,…,x_n]ω_{n+1}(x)
$$
$ω_{n+1}(x)$由(2.10)式定义
一阶差分:称$Δf_k=f_{k+1}-f_k$为xk处以h为步长的一阶(向前)差分
二阶差分:$Δ^2f_k=Δf_{k+1}-Δf_k$
xk处的n阶差分(3.8):$Δ^nf_k=Δ^{n-1}f_{k+1}-Δ^{n-1}f_k$
均差与差分的关系(3.11):
$$
f[x_k,…,x_{k+m}]=\frac{1}{m!}\frac{1}{h^m}Δ^mf_k,\quad m=1,2,…,n.
$$
差分与导数的关系(3.12):$Δ^nf_k=h^nf^{(n)}(ξ),其中ξ∈(x_k,x_{k+n})$
牛顿前插公式:(3.13)
$$
P_n(x_0+th)=f_0+tΔf_0+\frac{t(t-1)}{2!}Δ^2f_0+…+\frac{t(t-1)…(t-n+1)}{n!}Δ^nf_0
$$
前插公式余项:(3.14)
$$
R_n(x)=\frac{t(t-1)…(t-n)}{(n+1)!}h^{n+1}f^{(n+1)}(ξ),ξ∈(x_0,x_n)
$$
h为步长,$h^{n+1}$为步长的n次方,$f^{(n+1)}(ξ)$为函数的n+1阶导函数
形式差分表:

埃尔米特插值
重节点均差和泰勒插值
n阶重节点的均差:(4.1)
$$
f[x_0,x_0,…,x_0]=\lim_{x_i→x_0}f[x_0,x_1,…,x_n]=\frac{1}{n!}f^{(n)}(x_0)
$$
泰勒插值多项式(4.2):
$$
P_n(x)=f(x_0)+f’(x_0)(x-x_0)+…+\frac{f^{(n)}(x_0)}{n!}(x-x_0)^n
$$
它满足条件(4.3):
$$
P^{(k)}_n(x_0)=f^{(k)}(x_0),k=0,1,2,…,k
$$
其余项(4.4):
$$
R_n(x)=\frac{f^{n+1}(ξ)}{(n+1)!}(x-x_0)^{n+1},ξ∈(a,b)
$$
x∈[a,b]
两个典型的埃尔米特插值
第一种埃尔米特插值:满足条件(三个零点,一个一阶导数)
$$
P(x_i)=f(x_i)(i=0,1,2)及P’(x_1)=f’(x_1)
$$
插值多项式:
$$
P(x)=f(x_0)+fx_0,x_1+fx_0,x_1,x_2(x-x_1)+A(x-x_0)(x-x_1)(x-x_2)
$$
其中
$$
A=\frac{f’(x_1)-f[x_0,x_1]-(x_1-x_0)f[x_0,x_1,x_2]}{(x_1-x_0)(x_1-x_2)}
$$
余项(4.5):
$$
R(x)=\frac{1}{4!}f^{(n)}(ξ)(x-x_0)(x-x_1)^2(x-x_2)
$$
$ξ位于x_0,x_1,x_2和x所界定的范围内$
第二种埃尔米特插值:两点三次埃尔米特插值,插值节点取为xk及xk+1,插值多项式为H3(x),满足条件(4.6):
$$
\left. \begin{aligned}
&H_3(x_k)=y_k,&H_3(x_{k+1})=y_{k+1},\
&H_3’(x_{k})=m_{k+1},&H_3’(x_{k+1})=m_k
\end{aligned} \right }
$$
采用基函数方法,令(4.7)
$$
H_3(x)=α_k(x)y_k+α_{k+1}(x)y_{k+1}+β_k(x)m_k+β_{k+1}(x)m_{k+1}
$$
,其中$α_k(x),α_{k+1}(x),β_k(x),β_{k+1}(x)$为关于节点xk和xk+1的三次埃尔米特插值基函数,分别满足条件:
$$
α_k(x_k)=1,α_{k+1}(x_{k+1})=0,α’{k}(x_k)=α’{k}(x_{k+1})=0;\
α_{k+1}(x_{k})=0,α_{k+1}(x_{k+1})=1,α’{k+1}(x_k)=α’{k+1}(x_{k+1})=0;\
β_k(x_k)=β_k(x_{k+1})=0,β_{k}’(x_k)=1,β’{k}(x{k+1})=0;\
β_{k+1}(x_k)=β_{k+1}(x_{k+1})=0,β’{k+1}(x{k})=0,β’_{k+1}(x_{k+1})=1;
$$
求得,(4.8)(4.9)(4.10)(4.11)
$$
α_k(x)=(1+2\frac{x-x_k}{x_{k+1}-x_k})(\frac{x-x_{k+1}}{x_k-x_{k+1}})^2.\
α_{k+1}(x)=(1+2\frac{x-x_{k+1}}{x_{k}-x_{k+1}})(\frac{x-x_{k}}{x_{k+1}-x_{k}})^2.\
β_k(x)=(x-x_k)(\frac{x-x_{k+1}}{x_k-x_{k+1}})^2.\
β_{k+1}(x)=(x-x_{k+1})(\frac{x-x_{k}}{x_{k+1}-x_{k}})^2.\
$$
余项(4.13)
$$
R_3(x)=\frac{1}{4!}f^{(n)}(ξ)(x-x_k)^2(x-x_{k+1})^2 \quad,ξ∈(x_k,x_{k+1})
$$
分段低次插值
分段线性插值函数在每个小区间$[x_k,x_{k+1}]$上可表示为:(5.1)

误差估计:(5.2)
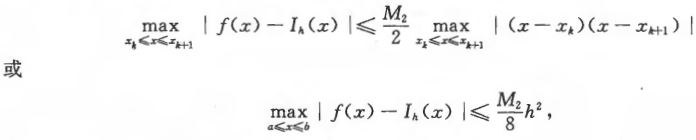

分段三次埃尔米特插值在每个小区间$[x_k,x_{k+1}]$上可表示为:(5.3)

误差估计:

三次样条插值
三次样条函数:

三次样条插值函数:(6.1)S(x)是三次样条函数

常见的3种边界条件:(6.3)、(6.4) 、(6.4)’ 、(6.5)

三次样条插值函数表达式:(6.8)

Mj(j=0,1,…,n)是未知的.且
逼近
函数逼近的定义:
范数
常用的三种范数:

内积
向量内积:(1.5)

函数内积(带权ρ(x)):(1.15)

特别地,当ρ≡1:

正交多项式
勒让德多项式:(2.5)

勒让德多项式递推关系:
(2.9)

第一类切比雪夫多项式:(2.10)

第二类切比雪夫多项式:(2.11)
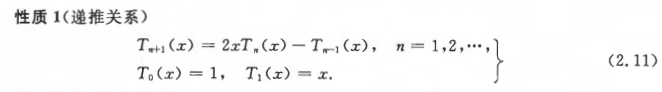
帕德逼近
帕德逼近定义:(5.7),(5.8)


求解帕德逼近系数:

(5.9) (5.11)


其中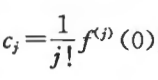
也就是泰勒展开第j项的系数的绝对值!
