机器学习作业1-过拟合

机器学习作业一过拟合

对“过拟合”的理解

从现象上来看,过拟合会导致训练的模型在训练的数据上预测的结果非常好,但是对训练集以外的数据却预测得不尽人意，甚至非常离谱。也就是模型由于“过度学习”，相当于对训练数据进行了“记忆”，而非“学习”，也就是俗话所说的”熟悉但不了解“。这种现象的发生的根本我想是因为这个世界的本质是概率和随机的，所以训练集的数据不可避免地无法全面地反映出规律，或者说具有偶然性（噪声和异常值），所以对数据的过拟合会使模型反而偏离了真正的规律，也就降低了其泛化能力。

正则化缓解过拟合

正则化可以缓解过拟合的原因在于它通过限制模型的复杂性来约束参数的取值范围，从而提高了模型的泛化能力。

以线性回归为例，没有正则化的情况，它的损失函数是平方损失函数，如果拟合函数h越复杂，就越可能把损失拟合到0，就会发生过拟合。

正则化方法是在损失函数中加入另一个由模型参数构造的函数来抑制过于逼近的问题，从而降低模型对训练数据的过度拟合，提高模型的泛化能力。
不论是L1正则化还是L2正则化，都是在优化目标函数的过程中加入了一个正则项，用于限制模型参数的取值范围。L1正则化倾向于产生较小的系数，L2正则化则惩罚系数平方的和。这两种正则化方法都可以通过控制模型的复杂性来防止过拟合，从而提高模型的泛化能力。

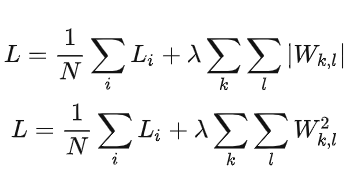
上面是正则化后目标函数的抽象模型（上为L1正则化，下为L2正则化），是在原本损失函数的基础上添加了正则化项（加号后面的）。对于逻辑回归模型，则为

$$
L_1=-\frac{1}{m}log(L(θ))+\frac{λ}{m}\sum|θ|
$$

$$
L_2-\frac{1}{m}log(L(θ))+\frac{λ}{2m}\sumθ^2
$$

对于L1正则化，损失函数为：

$$
J(\omega)
=-\frac{1}{m}\sum^m_{i=1}{lnP(y_i|x_i,\omega)}+\fracλm\sum^m_{i=1}|ω_i|\
=-\frac{1}{m}\sum^m_{i=1}ln(y_i\frac{1}{1+e^{-\omega^T x_i}}+(1-y_i)\frac{e^{-\omega^T x_i}}{1+e^{-\omega^T x_i}})+\fracλm\sum^m_{i=1}|ω_i|
$$

同理，L2正则化损失函数为：

$$
J(\omega)
=-\frac{1}{m}\sum^m_{i=1}{lnP(y_i|x_i,\omega)}+\fracλ{2m}\sum^{m}{i=1}ω_i^2\
=-\frac{1}{m}\sum^m{i=1}ln(y_i\frac{1}{1+e^{-\omega^T x_i}}+(1-y_i)\frac{e^{-\omega^T x_i}}{1+e^{-\omega^T x_i}})+\fracλ{2m}\sum^m_{i=1}ω_i^2
$$

其中L1正则化梯度的下降偏导公式为

$$
\frac{\partial J}{\partial \omega_j}=\frac{1}{m}\sum_{i=1}^m x_{ij}(\frac{e^{\omega^T x_i}}{1+e^{\omega^T x_i}}-y_i)+\fracλm
$$

L2正则化梯度下降偏导公式为

$$
\frac{\partial J}{\partial \omega_j}=\frac{1}{m}\sum_{i=1}^m x_{ij}(\frac{e^{\omega^T x_i}}{1+e^{\omega^T x_i}}-y_i)+\fracλm\sum^m_{i=1}|ω_i|
$$

参数更新的公式为

$$
\omega_j =\omega_j-\eta\frac{\partial J}{\partial w_j}
$$

其中

$\eta$表示学习率，$m$则表示批量中的样本数量，$x_{ij}$代表着第i个样本的第j个特征值,$y_i$代表着第i个样本的真实值

可以如下实现梯度下降法(L1正则化）：

def sigmoid(x):
    return 1/(1+np.exp(-x))
def gradient_descent(X, y, learning_rate, num_iterations, lambda_param):  
    m, n = X.shape  
    w = np.ones(n+1)
    X = np.hstack((np.ones((m,1)),X))
    for i in range(num_iterations):
        h = sigmoid(X.dot(w))
        error = h - y
        # compute the gradient  
        gradient = - (1 / m) * X.T.dot(error) + lambda_param / m

对于L2正则化，只要gradient=- (1 / m) * X.T.dot(error) + lambda_param* np.absolute(w).sum()/ m